This article (and many other great training articles) was written by my friend and great educator Jamie Kitchen. This article was originally posted on LinkedIn HERE and has been republished for your benefit with his permission. Thanks, Jamie!

I remember back in college I was immersed in a particularly challenging problem dealing with poly-phase circuits. At the time I was fighting back the urge to adopt the cop-out attitude of “When will I ever need this anyways” and trying hard to see the big picture of what was actually going on in the circuit. Probably a good idea since I had already shelled out $47.95 for the Lister textbook in 1986 dollars. As it turned out, this problem became the foundation for a lot of what I train others on today and also helped me solve problems for others to figure out why current or voltage readings were not the value they were supposed to be. The main culprit was usually power quality whether it was low voltage or poor power factor.

As a technician, we are charged with finding the solution to problems and then coming up with a way to put that solution into action that will ensure the customer does not have this problem again, at least not in the near future anyway. However, when it comes down to power quality, a lot of the solutions fall outside of our jurisdiction to take action. This is due to the fact that the problem is usually created and thus needs to be solved on the other side of the disconnect. What we need to do though is inform the customer of the issue and stress that if it is not solved, then replacing a compressor or other electrical components will only be a short-term solution and an expensive one at that.

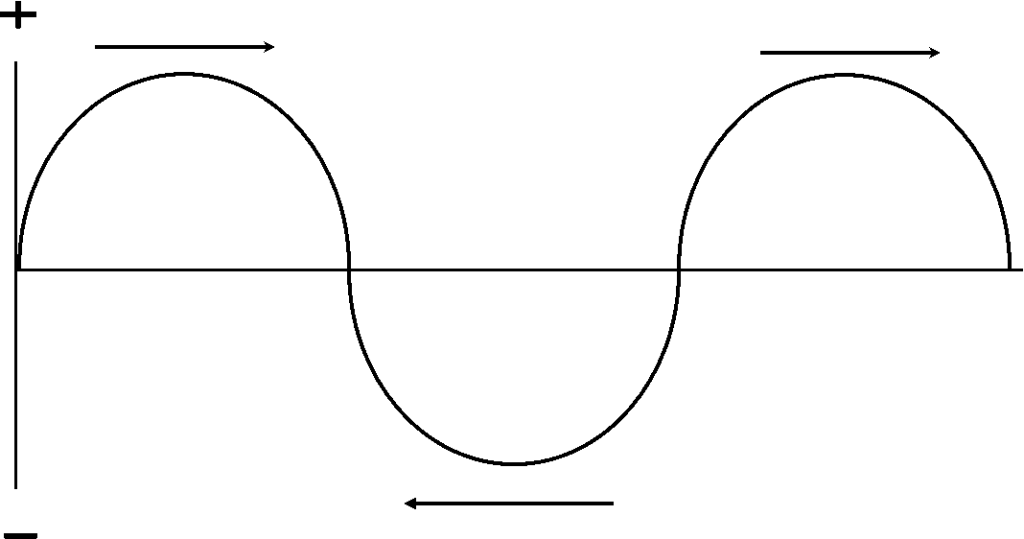
Let's take a look at what determines the ‘Quality' of electrical power because that is really the only way that you will have the necessary toolkit to understand and take action in the future. To start, we need to look at the sine wave. Alternating Current (AC) electricity is generated with rising and falling values for voltage and current that cycle 60 times per second here in North America, or 50 times a second over in Europe. If we draw a horizontal line that represents a zero value for voltage with time moving to the right, as the value of the voltage rises over time, it creates a curve on the positive side of the zero line which is above it. When it reaches it's maximum value it then starts to fall as it continues to move to the right. It eventually hits the horizontal zero line and continues on its way into negative territory until it once again reaches its maximum value. From here it heads back up to the zero line. When it hits zero, it has made one cycle. It will do 50 or 60 of these cycles in each second. A negative value for voltage simply means it is pushing in the opposite direction to the way it was when it was positive.

As we learned in school, voltage is the pressure that causes current to flow against a resistance. As voltage increases for a given resistance, the value of the current will also increase in lockstep. This occurs when the current and voltage are moving through a pure resistance (More on this in a second.) In this type of circuit then, both voltage and current make their own sine waves,  (Hopefully) each rising and falling together (Albeit with different values.) The voltage and current are completely in phase with each other. Ohms law dictates that in this type of circuit, power in watts is equal to volts x amps (P = V*I). If an electric resistance heater consumes 10 amps at 120 volts, then it's power consumption is = 120 volts *10 amps = 1200 watts. It also has a resistance of R=V/I = 120/10 = 12 ohms.

So far so good. However, there is another factor that comes into play with AC electricity and it is called Impedance. As its name implies, it can be a real roadblock in trying to figure out why an AC circuit is not acting like we were taught when we first took Ohms Law back in school. It has everything to do with the nature of AC power and the rising and falling of the voltage and current values over time we discussed above. When we use direct current where the voltage value is steady and constant at the supply, Impedance does not really come into play except when the values rise and fall when the power supply is turned off and on respectively. However, when you have a changing value of voltage and a rapid one at that, strange things begin to happen in the electric circuit that we may not familiar with. On top of that, they can actually be the dominant factors at play and by a very large margin.

When we first had the students build simple electric circuits with the power being supplied by the 120-volt wall receptacles, we would have them measure the resistance of a small motor and then using ohms law, have them calculate the expected current. If the motor had a resistance of say 8 ohms, they would come up with a current value of 15 amps which is pretty impressive when you consider it was a 1/20 hp motor. Of course, once they energized the circuit they would measure something like .5 amps and would then puzzle over what happened. Looking back, I can't think of a better segue for beginning AC power instruction than this one as they now have actual test data to work with and to use in their calculations. The answer to their puzzle is that they just witnessed an effect of AC power, inductive reactance, and Impedance.

Impedance is the combined effect of resistance and reactance, both of which can be found in an AC circuit. It is measured in ohms just like resistance but unlike resistance, it can be manipulated by changing different variables such as the number of capacitors in the system as well as the frequency of the electrical power. In addition, there are 2 types of reactance, inductive and capacitive. More on these below.

Once they learned the formulas for calculating capacitive and inductive reactance, they could then calculate impedance and the answer would be in ohms and it would tell them exactly why the current they measured for the small motor was so low. The actual resistance in the circuit was only a small part of the total opposition to current flow. Without getting into the heavy math, we can show the effects of inductive and capacitive reactance on a circuit (And also demonstrate why run capacitors are found on a lot of motors. ) and why the power that is being supplied to that compressor may not doing as much work as it should be. It all has to do with those voltage and current sine waves and how they rise and fall in relation to each other.

To put it simply, capacitive reactance causes the current value to rise and fall ahead of the voltage value (Current leads the voltage.) due to how capacitance stores and then releases current as the value of the voltage applied to a capacitor begins to drop in value. As the voltage drops, the internal pressure of the electrons stored in the capacitor becomes greater than the voltage applied to it and they begin to flow out, increasing the number of electrons and thus the current flowing in the circuit even as the voltage begins to fall. The catch is that the electrons are flowing in the opposite direction that the voltage is trying to push them so the current value will actually increase past the zero value and begin to flow in the opposite direction ( Have a negative or positive value) before the voltage does.

Inductive reactance results from a coil such as that of a motor winding, inducing a voltage of its own, separate from the one that is being applied by the power source. It is in effect then acting as a generator. A coil induces a voltage due to the effect that a moving magnetic field induces a voltage (Potential) in a conductor that is moving relative to it. In the case of an AC circuit, the rising and falling current results in a rising and falling magnetic field around the conductors carrying the current. What many may not realize is that magnetic field lines actually move away and towards the conductor. Any conductor nearby, is also moving through the magnetic field lines or more accurately, the field lines are moving past it. Since an electric motor is basically a lot of conductor wire wound tightly around itself, the falling and rising magnetic field that results in an AC circuit induces a voltage in any conductors nearby which is pretty much all of them in a motor. Now here is the catch, the induced voltage is opposite to the one that is being supplied by the power source. This means it opposes it and reduces its effect.

Based on the explanation in the previous paragraph, the induced voltage essentially cancels out a large part of the voltage being applied to the motor due to it having the opposite force. If the applied voltage is 120 volts, and the motor produces a back EMF of 116 volts, that only leaves 4 volts to overcome the 8-ohm resistance of the small 1/20 hp motor that was used in the electrical lab mentioned above. Since I = V/R, we get 4/8 =.5 amps which is what the students actually measured.

Another thing to point out is that the effect of inductive reactance is opposite to the effect of capacitive reactance that is it causes the current to lag the voltage. In a circuit with a large number of electric motors and no capacitors are installed, the current will lag the voltage and this will cause issues in how well the actual power supplied to the motors can be used. And the effect will not be good to put it mildly. The bottom line is that since power is the product of voltage and current multiplying together, if the current value is not in phase with the voltage, the resulting values from multiplying them together will not be as high as if they are in phase.

To continue, we need to introduce a value known as RMS or Root Mean Square. It is the value determined by averaging the squares of many instantaneous measurement values from the sine wave curve/s. If the current sine wave is out of phase with the voltage sine wave, then they will not rise and fall at the same time. If you take a lot of measurements of the value of the voltage along its sine wave, and then measure the value of the current at the same periods in time, the value of the current will be lower than it should be if the sine waves were perfectly aligned (In phase. ) Since the RMS values of the current and voltage are determined by taking a lot of measurements together, their RMS values will also be lower than they should be. The resulting power calculated then will also be lower since RMS values for voltage and current are used in calculating power.

This brings in power factor. Power factor is essentially the ratio between the value of power calculated using voltage and current values completely in phase with each other and the value calculated using the actual values present in the system. The more the current and voltage RMS values are out of phase, the lower the power factor value will be. If you do the math and you arrive at a power factor value of .85, then it means that only 85% of the current can actually be used by the motor and the other 15% is wasted (Usually as heat.)

To reiterate then, power is what the motor requires to overcome a load. With a power factor of .85, only 85% of the current is available for the motor to use for power. As a result, it requires more current to make the required power it needs to overcome the load. This load is created by the compression ration and will not drop just because there is not enough power being generated with the supplied current. As a result, more current must flow to make up for the poor quality of the power factor. In this case, 1/.85 = 17.5% more current. If the compressor drew 20 amps with perfect power factor, then it would draw 23.5 amps with a power factor value of .85 to make the same power from the electricity.

Here is the thing: the power company charges you for the power you consume, not the value that your motors can actually make use of. In other words, you get charged for the power calculated using 23.5 amps times the voltage so your power bill also goes up 17.5%. Oh, and many utilities also penalize you heavily if your power factor is below a certain value so it behooves anyone who operates equipment that uses electricity to make sure that they have good power quality. This is where our friend the capacitor makes its debut. Capacitance has the opposite effect of inductance and they cancel each other out. This means that if you have a lot of motors in a building, adding capacitors to the circuits will greatly improve power factor value and bring them close to 1 which means that the RMS voltage and current values are close to ideal. This will reduce power consumption and increase efficiency greatly.

If a technician encounters current values higher than what the measured voltage and load conditions warrant, there is a good chance that power factor may not be as high as it should be. This must be brought to the attention of the owner so it can be corrected. However, unless it is a simple manner of installing a run capacitor on the compressor/s, it likely falls outside of both the qualification as well as the responsibility of the technician unless of course they also have the necessary quantification's and are licensed to perform such procedures.

Given the cost to operate equipment that is using substantially more power than is necessary, not to mention the very real possibility of having to replace expensive components more often than is normally required, it should not be hard to get your message across. A data logger or even some simple math demonstrating the costs vs. savings can be a powerful tool.

—Jamie Kitchen