Capacitors are traditionally tested with a capacitance meter (commonly found as a function within a multimeter), with the component taken entirely out of the circuit. “Bench testing,” as this method is referred to, is hands-down the safest method of checking capacitance in microfarads. All other methods require the capacitor to be wired into the circuit with an applied load. To bench test, you simply take the meter leads and check across the terminals of the capacitor. For a dual-run capacitor, you would check between the Common terminal and whichever side (Fan or Herm) you wish to test.

Another popular test many technicians use is the “under load capacitance calculation.” We perform this test while the system is in normal operation. A technician would measure the voltage across the terminals of the capacitor (again, Common and Motor terminals if dual-run), then measure the current off the start winding of the motor to which the capacitor is attached. Next, you plug those values into a calculation, which uses a mathematical constant: (amps x 2,652) ÷ voltage. Finally, we compare the product of that calculation against the rated capacitance printed on the capacitor. As long as the calculated value is within +/- 6% of the rated value, the capacitor quality is acceptable.

Bench testing and capacitance calculations are pretty popular choices when verifying the capacitance of a capacitor against its rating. However, there is yet another way to test a capacitor under load you may not have thought of before. You can use a power quality meter to check the capacitor under load using the power factor. To explain the validity of this measurement, here is a review of reactive power, inductive loads, and capacitors.

Reactive power is one of three different types of power in an alternating current circuit. True power is the actual energy in watts dissipated by a circuit; it is the real work being done. Then there is apparent power, measured in volt-amps (VA). Apparent power is the RMS current multiplied by the RMS voltage. Reactive power is the power dissipated as a result of either inductive or capacitive loads. We measure reactive power in volt-amps reactive (VAr). When the current and voltage waveforms are out of phase with each other, that is reactive power. Inductive loads, such as a condenser fan motor, are inductive because their alternating current lags behind the alternating voltage as the current flows into the load. Capacitive loads have an alternating current waveform that leads the alternating waveform of the voltage.

For the purposes of this tech tip, we will exclusively discuss inductive loads because they are most common in the residential field (e.g., condenser, blower, and compressor motors). Inductive loads use a magnetic field to cause physical movement. The magnetic field is generated as electric current flows through a coil. In other words, this current/energy used to generate a magnetic field is known as reactive power. Notice, however, there is no real work being done. The force of the magnetic field can cause physical movement (work), but it does no real work itself. Inductive loads need reactive power to do work, but by using more and more reactive power, the load also uses more current (usually from the utility company). Take a look at the “power triangle” below.

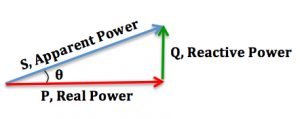Pictured is a power triangle depicting an inductive load. The hypotenuse of this triangle is notated as apparent power (the available power in the circuit). The leg on the y-axis is notated as reactive power (magnetic field), and the leg on the x-axis is notated as real power (actual work being done). If you notice the Theta symbol in the left acute hypotenuse angle (𝜭), this refers to the power factor of the load. Power factor (cos𝜭) is the ratio of the average real power in watts to the apparent power in volt-amps. Ideally, the apparent and real power would be the same, as in a resistive load (i.e., a power factor of 1). However, inductive loads need a magnetic field.

If the reactive power leg on the y-axis were to increase and rise higher on the y-axis, the hypotenuse (apparent power) would also increase. The power factor, in this case, decreases and moves closer and closer to the left acute hypotenuse angle, thereby increasing the distance between the apparent power and real power. This is counter-productive because as the load uses more current, more heat energy is generated, and the energy used to do the actual work becomes inefficient.

Therefore, the engineer aims to minimize the amount of reactive power the inductive load uses from the apparent power. Basically, the goal is to increase the power factor back to as close to unity (1) as possible. That is when capacitors come on the scene.

Capacitors are generally accepted as reactive power generators. To understand how capacitors work and clear up some common misconceptions, check out these other tech tips/podcast episodes: Run Capacitor Facts You May Not Know (Podcast) & 5 Capacitor Facts You Should Know.

When applied to a circuit, capacitors decrease the amount of apparent power needed by the inductive load to generate the magnetic field. This effectively increases the power factor. Looking at the power triangle again, as the reactive power on the y axis decreases, the hypotenuse (apparent power) also decreases, moving closer to the real power. This is the endgame for capacitors.

Therefore, we can infer from the understanding of inductive loads and capacitors that if a capacitor is attached to an AC circuit in an inductive load (like a PSC motor) to bring the power factor back to as close to unity as possible, but the power factor is determined to be low, the capacitor must then be either sized incorrectly or failing/failed.

Using a power quality meter on an inductive load, a technician can judge the functionality of a particular capacitor. To do this, you must measure voltage and current simultaneously at the load. The Supco Redfish iDVM-550 is a great tool for this application.

I must also mention that using a power quality meter to measure the power factor on a load is valid only when the load contains run capacitors, like compressors and permanent-split capacitor motors. ECMs (electronically commutated motors) use a different type of technology altogether, and they are engineered for use with a lower power factor by design. Also, power factor testing is not practical for start capacitors either since the capacitor is taken out of the circuit too quickly. This measurement is valid and practical only for PSC-type blowers, condenser motors, and most single-phase and single-stage compressors.