October 2018

Here is another excellent article from Michael Housh, owner of Housh Home Energy and a regular contributor to HVAC School. Thanks, Michael! I thought I would go through a simple example of sizing a hydronic circulator for an application. This is a made-up scenario, but I sketched out a 20’ x 20’ square home with […]

This episode is about a simplified way to explain the basic refrigerant circuit to new techs that may help lock in the basic idea of absorbing and rejecting heat

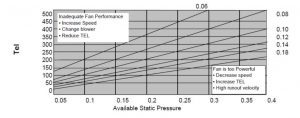
This article is written by one of the smartest guys I know online, Neil Comparetto. Thanks, Neil! Recently, I posted a question in the HVAC School Group on Facebook that went like this: “When designing a residential duct system, what friction rate do you use?” As of writing this, only one answer was correct according […]

This article was written by Michael Housh, owner of Housh Home Energy and a regular contributor to HVAC School. Thanks, Michael! This is another article in trying to relate the air side of HVAC with the water side. In this article, I’m going to talk about how to determine pump flow (GPM) based on the […]

In this part one of the two part combustion analysis series Jim Bergmann covers CAZ testing or Worst-Case Draft and Pressure Testing in detail and why it matters to techs and customers

In this episode we talk about what it REALLY takes to setup and commision a new system properly

In my recent classes with my employees at Kalos, we've been going over finding target pressures and temperatures for an air conditioning system. The goal has been to get techs to have “target” readings in mind before they start connecting tools. This step is an important part of being able to “check a system without […]

In this episode Rusty Walker from Hill Phoenix talks through the three most common types of market CO2 systems and how they work. Secondary, Cascade and Booster.

Can you really trust that temperature reading? In this short episode we talk aout some common mistakes techs make in making temperature measurements and what to do about it.